5 Go语言中的矩阵和向量计算

矩阵和向量计算在计算机科学中非常重要。向量可以在动态数组中存储一组对象，它采用连续存储方式，并且能够灵活调整以适应数据的增长。矩阵则是基于向量构建的，形成了二维向量集合。在本章中，我们将探讨矩阵和向量，以及这两种数据结构在实际应用中如何用于进行当今计算机科学领域中的大量数据处理操作。向量和矩阵是线性代数常用的基础结构，而线性代数在现代计算机科学中至关重要。诸如图像处理、计算机视觉和网络搜索等过程都会借助线性代数来实现各自的功能。

在本章中，你将学习以下主题：

• 基本线性代数子程序（Basic Linear Algebra Subprograms，BLAS）
• 向量
• 矩阵
• 向量和矩阵操作

一旦我们将这些内容融会贯通，你就会明白矩阵和向量计算的不同方面是如何推动大规模数据的高效处理的。

介绍Gonum和Sparse库

Gonum包是Go语言中用于科学算法的最受欢迎的库之一。Gonum包（https://github.com/gonum ）提供了一些工具，帮助我们使用Go语言编写高效的数值算法。这个包专注于创建高性能算法，以应用于各种不同的场景，向量和矩阵是该包的核心内容。创建这个库时就充分考虑了性能因素，其开发者发现用C语言实现向量化存在问题，因此构建了这个库，以便在Go语言中更轻松地处理向量和矩阵。Sparse库（https://github.com/james-bowman/sparse ）是在Gonum库的基础上构建的，用于处理机器学习和其他科学计算领域中常见的稀疏矩阵操作。在Go语言中，结合使用这两个库是管理向量和矩阵的高效方式。

在下一节中，我们将了解什么是BLAS。

介绍BLAS

BLAS是一种常用于执行线性代数运算的规范。这个库最初是1979年用FORTRAN语言编写的，从那以后一直持续维护。BLAS针对矩阵的高效操作进行了大量优化。由于该规范的深度和广度，许多语言都选择将其作为各自领域内线性代数库的一部分。Go语言的Sparse库在进行线性代数运算时就采用了BLAS的实现方式。BLAS规范由三个不同的例程组成：

• 一级（Level 1）：向量运算
• 二级（Level 2）：矩阵 - 向量运算
• 三级（Level 3）：矩阵 - 矩阵运算

这些分级例程有助于规范的实现和测试。BLAS在许多实现中都有应用，从Accelerate（适用于macOS和iOS的框架）到英特尔数学核心库（Intel Math Kernel Library，MKL），它已成为应用计算机科学中线性代数不可或缺的一部分。现在，是时候了解向量了。

介绍向量

向量是一维数组，通常用于存储数据。Go语言原本有container/vector实现，但在2011年10月18日被移除了，因为切片被认为在Go语言中用于向量更为合适。Go语言内置切片提供的功能对向量操作有很大帮助。切片可以用来实现行向量，即1×m矩阵。一个简单的行向量如下所示：

如你所见，这是一个1×m矩阵。在Go语言中，我们可以使用切片表示法来实现一个简单的行向量，如下所示：

v := []int{0, 1, 2, 3}

这是利用Go语言内置功能表示简单行向量的简便方法。

向量计算

列向量是m×1矩阵，也被称为行向量的转置。矩阵转置是指将矩阵沿对角线翻转，通常用上标T表示。我们可以在下图中看到列向量的示例：

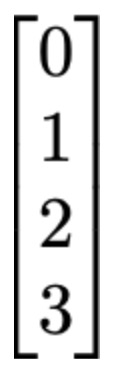
如果我们想在Go语言中实现一个列向量，可以使用Gonum向量包来初始化这个向量，如下代码块所示：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    v := mat.NewVecDense(4, []float64{0, 1, 2, 3})
    matPrint(v)
}

func matrixPrint(m mat.Matrix) {
    formattedMatrix := mat.Formatted(m, mat.Prefix(""), mat.Squeeze())
    fmt.Printf("%v\n", formattedMatrix)
}

这段代码会打印出与上图类似的列向量。

我们还可以使用Gonum包进行一些巧妙的向量操作。例如，在下面的代码块中，我们可以看到将向量中的值翻倍是多么简单。我们可以使用AddVec函数将两个向量相加，从而得到一个翻倍的向量。我们还有prettyPrintMatrix辅助函数，使矩阵更易于阅读：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    v := mat.NewVecDense(5, []float64{1, 2, 3, 4, 5})
    d := mat.NewVecDense(5, nil)
    d.AddVec(v, v)
    fmt.Println(d)
}

func prettyPrintMatrix(m mat.Matrix) {
    formattedM := mat.Formatted(m, mat.Prefix(""), mat.Squeeze())
    fmt.Printf("%v\n", formattedM)
}

这个函数的结果，即翻倍后的向量，如下所示：

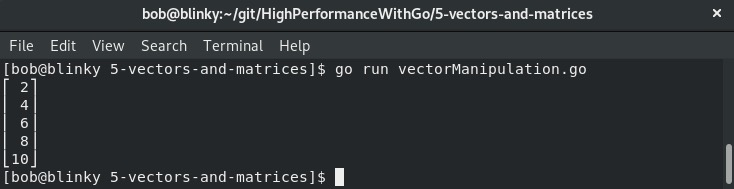
gonum/mat包还为向量提供了许多其他实用的辅助函数，包括：

• Cap()：返回向量的容量
• Len()：返回向量中的列数
• IsZero()：验证向量是否为空
• MulVec()：将向量a和b相乘并返回结果
• AtVec()：返回向量中指定位置的值

gonum/mat包中的向量操作函数帮助我们轻松地将向量处理成所需的数据集。

既然我们已经了解了向量，现在来看看矩阵。

介绍矩阵

矩阵是二维数组，由行和列进行区分。矩阵在图形处理和人工智能（尤其是图像识别）领域非常重要。矩阵常用于图形处理，这是因为矩阵中的行和列可以与屏幕上像素的行列排列相对应，而且矩阵的值可以对应特定的颜色。矩阵也经常用于数字声音处理，因为数字音频信号通过傅里叶变换进行滤波和压缩，而矩阵有助于实现这些操作。

矩阵通常用M×N的命名方式表示，其中M是矩阵的行数，N是矩阵的列数，如下图所示：

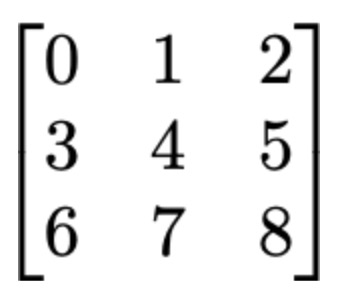
例如，上图是一个3×3矩阵。M×N矩阵是线性代数的核心概念之一，因此了解其关联非常重要。

现在，让我们看看矩阵是如何运算的。

矩阵运算

矩阵是一种高效存储大量信息的方式，但矩阵的真正价值在于对其进行的操作。最常用的矩阵操作技术如下：

• 矩阵加法
• 矩阵数乘
• 矩阵转置
• 矩阵乘法

能够对矩阵执行这些操作非常重要，因为它们有助于大规模处理现实世界中的数据。在接下来的部分，我们将探讨其中一些运算及其实际应用。

矩阵加法

矩阵加法是将两个矩阵相加的方法。假设我们想求出两个二维集合相加的结果。如果有两个大小相同的矩阵，就可以将它们相加，如下所示：

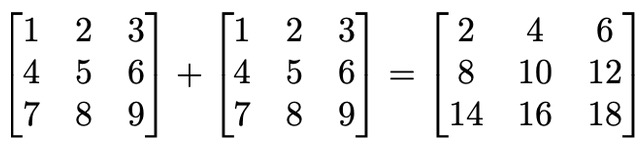
我们也可以用Go代码表示，如下代码块所示：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    a := mat.NewDense(3, 3, []float64{1, 2, 3, 4, 5, 6, 7, 8, 9})
    a.Add(a, a) // 将a和a相加
    matrixPrint(a)
}

func matrixPrint(m mat.Matrix) {
    formattedMatrix := mat.Formatted(m, mat.Prefix(""), mat.Squeeze())
    fmt.Printf("%v\n", formattedMatrix)
}

执行这个函数的结果如下：

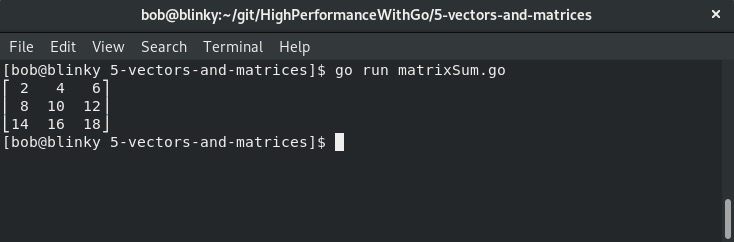
结果展示了代码块中矩阵相加的运算结果。

在下一节中，我们将讨论一个矩阵操作的实际示例。为了演示这个示例，我们将使用矩阵减法。

实际示例（矩阵减法）

假设你拥有两家餐厅，一家在纽约州纽约市，另一家在佐治亚州亚特兰大市。你想弄清楚每个月在你的餐厅中哪些菜品最畅销，以便确保在接下来的几个月里储备正确的食材。我们可以利用矩阵减法来计算每家餐厅每种菜品的净销售数量。我们需要有每家餐厅的销售原始数据，如下表所示：

五月销售数量：

	纽约，NY	亚特兰大，GA
龙虾浓汤	1345	823
田园沙拉	346	234
肉眼牛排	843	945
冰淇淋圣代	442	692

六月销售数量：

	纽约，NY	亚特兰大，GA
龙虾浓汤	920	776
田园沙拉	498	439
肉眼牛排	902	1023
冰淇淋圣代	663	843

现在，我们可以使用以下矩阵减法计算这两个月销售数量的差异：

我们可以在Go语言中执行相同的操作，如下代码块所示：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    a := mat.NewDense(4, 2, []float64{1345, 823, 346, 234, 843, 945, 442, 692})
    b := mat.NewDense(4, 2, []float64{920, 776, 498, 439, 902, 1023, 663, 843})
    var c mat.Dense
    c.Sub(b, a)
    result := mat.Formatted(&c, mat.Prefix(""), mat.Squeeze())
    fmt.Println(result)
}

我们得到的输出结果是两家餐厅五月和六月销售数量的差异，如下所示：

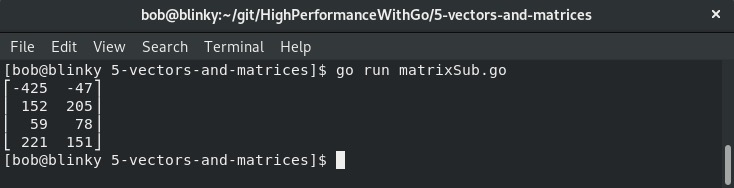
上图中的结果以N×M矩阵的形式展示了销售差异。

随着餐厅数量的增加和餐厅菜单上菜品的增多，利用矩阵减法将有助于我们记录需要储备哪些菜品。

标量乘法

在操作矩阵时，我们可能希望将矩阵中的所有值与一个标量相乘。

在Go语言中，我们可以用以下代码表示：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    a := mat.NewDense(3, 3, []float64{1, 2, 3, 4, 5, 6, 7, 8, 9})
    a.Scale(4, a) 
    matrixPrint(a)
}

func matrixPrint(m mat.Matrix) {
    formattedMatrix := mat.Formatted(m, mat.Prefix(""), mat.Squeeze())
    fmt.Printf("%v\n", formattedMatrix)
}

这段代码产生以下结果：

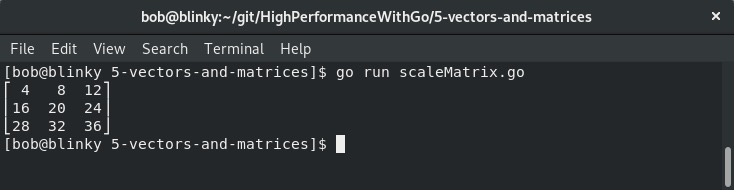
在这里，我们可以看到矩阵中的每个元素都被乘以了4，这是矩阵缩放的一个执行示例。

标量乘法的实际示例

假设我们拥有一家五金店，店里有一系列产品，每个产品都有对应的美元（USD）价格。公司决定不仅在美国销售产品，还将在加拿大销售。在撰写本书时，1美元相当于1.34加元（CAD）。我们可以看看基于数量的螺丝、螺母和螺栓的价格矩阵，如下表所示：

	单个（美元）	100个（美元）	1000个（美元）
螺丝	$0.10	$0.05	$0.03
螺母	$0.06	$0.04	$0.02
螺栓	$0.03	$0.02	$0.01

如果我们使用矩阵标量乘法来计算加元价格，最终会得到以下矩阵计算结果：

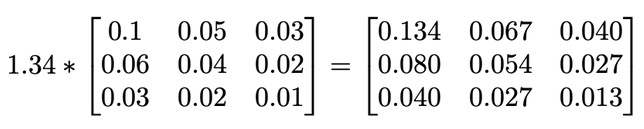
我们可以用Go语言的标量乘法功能来验证这一点，如下代码片段所示：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    usd := mat.NewDense(3, 3, []float64{0.1, 0.05, 0.03, 0.06, 0.04, 0.02, 0.03, 0.02, 0.01})
    var cad mat.Dense
    cad.Scale(1.34, usd)
    result := mat.Formatted(&cad, mat.Prefix(""), mat.Squeeze())
    fmt.Println(result)
}

我们得到一个结果矩阵，其中包含了每个产品的加元价格：

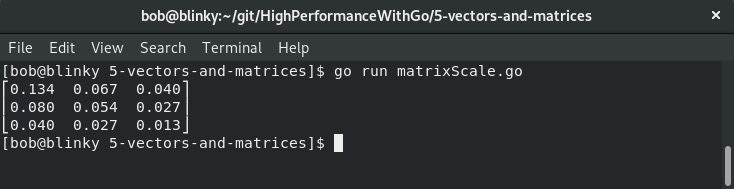
输出显示了缩放后的结果矩阵。

随着产品越来越多，涉及的货币种类也越来越多，矩阵标量操作将非常有用，因为它可以减少处理这些大量数据的工作量。

矩阵乘法

我们可能还想将两个矩阵相乘。两个矩阵相乘会得到它们的乘积。当我们希望以并发方式一次性将多个数字相乘时，这非常有用。我们可以取一个N×M的矩阵A和一个M×P的矩阵B。得到的结果集称为AB，是一个N×P的矩阵，如下所示：

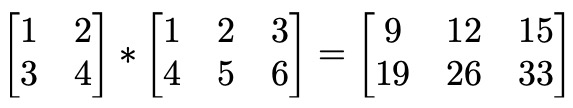
在Go语言中，我们可以用以下代码表示：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    a := mat.NewDense(2, 2, []float64{1, 2, 3, 4})
    b := mat.NewDense(2, 3, []float64{1, 2, 3, 4, 5, 6})
    var c mat.Dense
    c.Mul(a, b)
    result := mat.Formatted(&c, mat.Prefix(""), mat.Squeeze())
    fmt.Println(result)
}

执行后，我们得到以下结果：

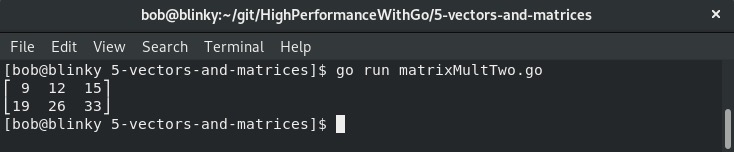
这就是我们使用gonum/mat包进行矩阵乘法的方法。矩阵乘法是一种常见的矩阵运算，理解如何进行矩阵乘法将有助于你有效地操作矩阵。

矩阵乘法的实际示例

让我们来讨论一个矩阵乘法的实际示例，以便将理论知识与实际应用联系起来。有两家电子供应商都希望为你的公司生产小部件。供应商A和供应商B都为小部件设计了产品方案，并提供了所需的零件清单。两家供应商使用相同的零件供应商。在这个例子中，我们可以使用矩阵乘法来确定哪家供应商生产的小部件成本更低。每个供应商提供的零件清单如下：

供应商A：

• 电阻：5个
• 晶体管：10个
• 电容器：2个

供应商B：

• 电阻：8个
• 晶体管：6个
• 电容器：3个

从零件供应商的产品目录中，你知道这些零件的价格如下：

• 电阻：每个0.10美元
• 晶体管：每个0.42美元
• 电容器：每个0.37美元

正如我们之前所学，我们可以用矩阵表示这些输入。具体如下：

1. 我们创建一个由零件成本组成的矩阵：
2. 我们创建一个由每个供应商所需零件数量组成的矩阵：
3. 然后，我们使用矩阵乘法得到一些有用的结果：

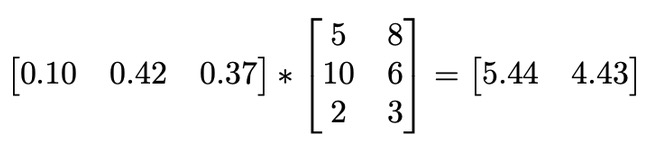
这个结果表明，供应商A的零件成本为5.44美元，而供应商B的零件成本为4.43美元。从原材料成本来看，供应商B的方案更便宜。

在Go语言中，可以用以下代码计算：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    a := mat.NewDense(1, 3, []float64{0.10, 0.42, 0.37})
    b := mat.NewDense(3, 2, []float64{5, 8, 10, 6, 2, 3})
    var c mat.Dense
    c.Mul(a, b)
    result := mat.Formatted(&c, mat.Prefix("    "), mat.Squeeze())
    fmt.Println(result)
}

输出结果证实了我们在前面计算的结果：

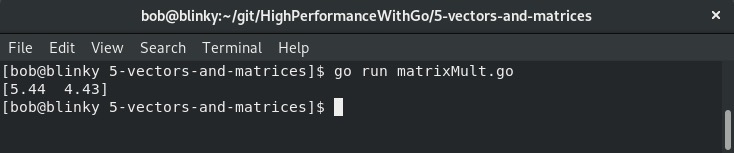
从结果中可以看出，格式化后的矩阵与我们之前的计算结果一致。通过实际示例有助于我们更好地理解理论概念。

矩阵转置

矩阵转置是将矩阵沿对角线翻转，交换行索引和列索引。下图展示了一个矩阵转置的示例：

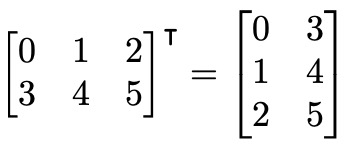
在Go语言中，我们可以用以下代码表示矩阵转置：

package main

import (
    "fmt"
    "gonum.org/v1/gonum/mat"
)

func main() {
    a := mat.NewDense(3, 3, []float64{5, 3, 10, 1, 6, 4, 8, 7, 2})
    matrixPrint(a)
    matrixPrint(a.T())
}

func matrixPrint(m mat.Matrix) {
    formattedMatrix := mat.Formatted(m, mat.Prefix(""), mat.Squeeze())
    fmt.Printf("%v\n", formattedMatrix)
}

矩阵转置的结果可以在下图中看到：

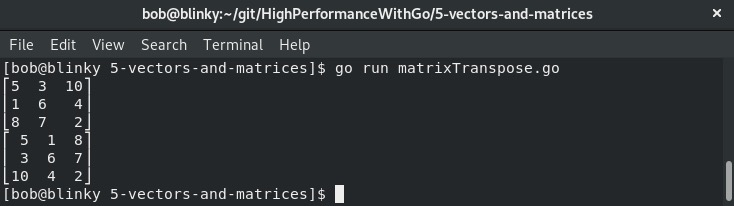
在上述输出中，我们可以看到原始矩阵和转置后的矩阵。在计算机科学中，矩阵转置常用于在内存中对矩阵进行转置，以提高内存局部性等。

矩阵转置的实际示例

矩阵转置很有趣，但了解矩阵转置在实际中的应用可能对你更有帮助。假设有三位工程师：鲍勃（Bob）、汤姆（Tom）和爱丽丝（Alice）。这三位工程师每天都会提交Git代码。我们希望以一种有意义的方式记录这些代码提交，以确保工程师们拥有继续编写代码所需的所有资源。我们统计三位工程师3天的代码提交次数：

用户	日期	提交次数
鲍勃	1	5
鲍勃	2	3
鲍勃	3	10
汤姆	1	1
汤姆	2	6
汤姆	3	4
爱丽丝	1	8
爱丽丝	2	7
爱丽丝	3	2

有了这些数据点后，我们可以用二维数组表示它们：

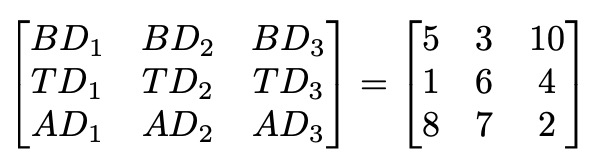
现在我们有了这个数组，可以对其进行转置：

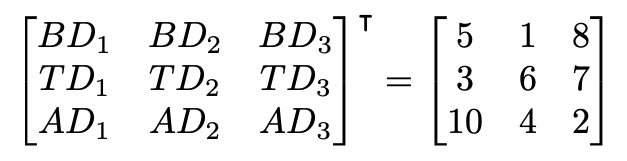
转置后，我们可以看到转置数组的行对应于提交代码的日期，而不是每个用户的提交。让我们看第一行：

现在，这一行代表BD1、TD1和AD1，即每个开发者在第1天的提交次数。

操作部分讲完了，现在是时候看看矩阵结构了。

理解矩阵结构

矩阵通常分为两种不同的结构：稠密矩阵和稀疏矩阵。稠密矩阵主要由非零元素组成。稀疏矩阵则主要由值为0的元素构成。矩阵的稀疏度通过零值元素的数量除以元素总数来计算。

如果该计算结果大于0.5，那么这个矩阵就是稀疏矩阵。这种区分很重要，因为它有助于我们确定矩阵运算的最佳方法。如果一个矩阵是稀疏矩阵，我们或许能够采用一些优化手段，让矩阵运算更高效。反之，如果是稠密矩阵，我们很清楚，很可能需要对整个矩阵进行运算。

要记住，在如今的计算机硬件条件下，矩阵运算很可能受限于内存。矩阵的大小是个需要重点关注的因素。在考虑何时使用稀疏矩阵或稠密矩阵时，要知道稠密矩阵中的一个int64类型的值，根据Go语言中数值类型的大小和对齐方式，占用8字节。而稀疏矩阵除了这个值，还需要一个int类型来表示该项的列索引。在选择使用哪种数据结构存储数据时，要把这些大小差异牢记于心。

稠密矩阵

创建稠密矩阵时，矩阵的所有值都会被存储。在某些情况下，这是不可避免的，比如当我们关注与某个表格相关的所有值，且该表格基本是满的。使用二维切片或数组来存储稠密矩阵通常是个不错的选择，但如果想要对矩阵进行操作，使用Gonum包能更有效地进行数据处理。实际上，大多数矩阵并不属于稠密矩阵这一类别。

稀疏矩阵

稀疏矩阵在现实世界的数据集中频繁出现。比如在电影目录中，某人是否观看过某部影片、在播放列表中听过多少歌曲，或者在待办事项列表里完成了哪些事项，这些场景都适合使用稀疏矩阵。这些表格中的许多值都是零，所以将这些矩阵存储为稠密矩阵并不合理，因为这会占用大量内存，而且运算成本高昂。

我们可以使用Go语言的稀疏矩阵库来创建和操作稀疏矩阵。这个稀疏矩阵库借鉴了基本线性代数子程序（BLAS）的惯例，能够执行许多常见的矩阵运算。Go语言的稀疏矩阵库与Gonum矩阵包完全兼容，因此可以与该包互换使用。在这个示例中，我们将创建一个新的键值对字典（Dictionary of Keys，DOK）形式的稀疏矩阵。创建完成后，我们会为数组中的集合设置特定的M×N值。最后，我们将使用gonum/mat包打印出创建的稀疏矩阵。

在下面的代码中，我们使用稀疏矩阵包创建一个稀疏矩阵。ToCSR()和ToCSC()矩阵函数分别用于创建压缩稀疏行（Compressed Sparse Row，CSR）矩阵和压缩稀疏列（Compressed Sparse Column，CSC）矩阵：

package main

import (
    "fmt"
    "github.com/james-bowman/sparse"
    "gonum.org/v1/gonum/mat"
)

func main() {
    sparseMatrix := sparse.NewDOK(3, 3)
    sparseMatrix.Set(0, 0, 5)
    sparseMatrix.Set(1, 1, 1)
    sparseMatrix.Set(2, 1, -3)
    fmt.Println(mat.Formatted(sparseMatrix))
    csrMatrix := sparseMatrix.ToCSR()
    fmt.Println(mat.Formatted(csrMatrix))
    cscMatrix := sparseMatrix.ToCSC()
    fmt.Println(mat.Formatted(cscMatrix))
}

执行这段代码后，我们可以看到返回的稀疏矩阵：

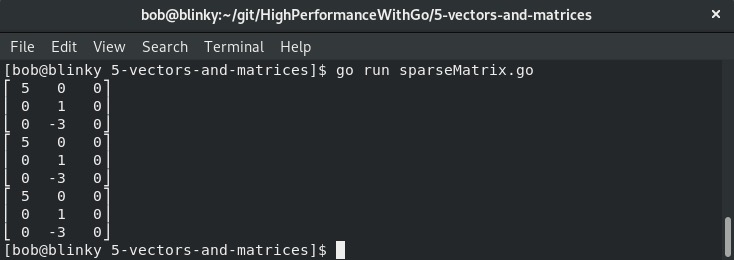
这个输出展示了生成的稀疏矩阵。

稀疏矩阵可以分为三种不同的格式：

• 用于高效创建和修改矩阵的格式
• 用于高效访问和矩阵运算的格式
• 特殊格式

用于高效创建和修改矩阵的格式如下：

• 键值对字典（Dictionary of Keys，DOK）
• 列表的列表（List of Lists，LIL）
• 坐标列表（Coordinate Lists，COO）

接下来的部分将对这些格式进行定义。

DOK矩阵

在Go语言中，DOK矩阵是一种映射（map）。这种映射将行和列的组合与它们相关联的值进行链接。如果矩阵中某个特定坐标没有定义值，那么该值被视为零。通常，哈希映射（hashmap）被用作底层数据结构，这使得随机访问的时间复杂度为O(1)，但遍历元素的速度会稍慢一些。DOK矩阵在矩阵构建或更新时很有用，但在进行算术运算时性能欠佳。创建好的DOK矩阵还可以轻松转换为COO矩阵。

LIL矩阵

LIL矩阵为每一行存储一个列表，该列表包含列索引和值，通常按列排序，这样可以减少查找时间。LIL矩阵在逐步构建稀疏矩阵时很有用。当我们不知道输入数据集的稀疏模式时，它也能派上用场。

COO矩阵

COO矩阵（也常被称为三元组格式矩阵）存储包含行、列和值的元组列表，并按行和列索引排序。向COO矩阵追加元素很简单，时间复杂度为O(1)。但从COO矩阵进行随机读取相对较慢（时间复杂度为O(n)）。COO矩阵是矩阵初始化和转换为CSR矩阵的不错选择。不过，它不太适合进行算术运算。通过对矩阵中的向量进行排序，可以提高对COO矩阵顺序迭代的性能。

用于高效访问和矩阵运算的格式如下：

• 压缩稀疏行（Compressed Sparse Row，CSR）
• 压缩稀疏列（Compressed Sparse Column，CSC）

接下来的部分将对这些格式进行定义。

CSR矩阵

CSR矩阵使用三个一维数组来表示一个矩阵。CSR格式使用以下三个数组：

• A：数组中存在的值。
• IA：每个值所在的索引。具体定义如下：
  • IA在索引0处的值，IA[0] = 0
  • IA在索引i处的值，IA[i] = IA[i - 1] +（原始矩阵第i - 1行的非零元素数量）
• JA：存储元素的列索引。

以下图片展示了一个4×4矩阵的示例。我们将在接下来的代码示例中使用这个矩阵：

我们可以这样计算这些值：

• A = [1 2 3 4]
• IA = [0 1 2 3 4]
• JA = [2 0 3 1]

我们可以使用稀疏矩阵包来验证这一点，如下代码片段所示：

package main

import (
    "fmt"
    "github.com/james-bowman/sparse"
    "gonum.org/v1/gonum/mat"
)

func main() {
    sparseMatrix := sparse.NewDOK(4, 4)
    sparseMatrix.Set(0, 2, 1)
    sparseMatrix.Set(1, 0, 2)
    sparseMatrix.Set(2, 3, 3)
    sparseMatrix.Set(3, 1, 4)
    fmt.Print("DOK Matrix:\n", mat.Formatted(sparseMatrix), "\n\n") // 键值对字典
    fmt.Print("CSR Matrix:\n", sparseMatrix.ToCSR(), "\n\n")        // 打印矩阵的CSR版本
}

结果展示了我们创建的矩阵的DOK表示形式的转换值，以及相应的CSR矩阵：

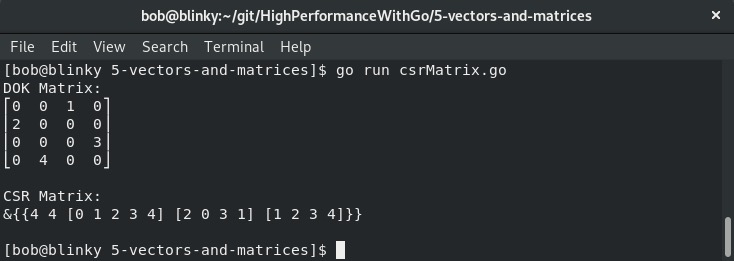
这段代码的输出展示了一个CSR矩阵，分别打印了IA、JA和A的值。随着矩阵规模的增大，能够计算CSR矩阵会让矩阵运算越来越高效。在计算机科学领域，经常需要处理具有数百万行和列的矩阵，因此，高效地进行这些操作能让代码的性能大幅提升。

CSC矩阵

CSC矩阵的格式与CSR矩阵基本相同，但有一个小差别。CSC矩阵压缩的是列索引切片，而不是像CSR矩阵那样压缩行索引切片。这意味着CSC矩阵按列主序存储值，而不是行主序。这也可以看作是CSR矩阵的自然转置。我们可以基于上一节的示例来看看CSC矩阵是如何创建的，如下代码块所示：

package main

import (
    "fmt"
    "github.com/james-bowman/sparse"
    "gonum.org/v1/gonum/mat"
)

func main() {
    sparseMatrix := sparse.NewDOK(4, 4)
    sparseMatrix.Set(0, 2, 1)
    sparseMatrix.Set(1, 0, 2)
    sparseMatrix.Set(2, 3, 3)
    sparseMatrix.Set(3, 1, 4)
    fmt.Print("DOK Matrix:\n", mat.Formatted(sparseMatrix), "\n\n") // 键值对字典
    fmt.Print("CSC Matrix:\n", sparseMatrix.ToCSC(), "\n\n")        // 打印CSC版本
}

结果展示了我们创建的矩阵的DOK表示形式的转换值，以及相应的CSC矩阵：

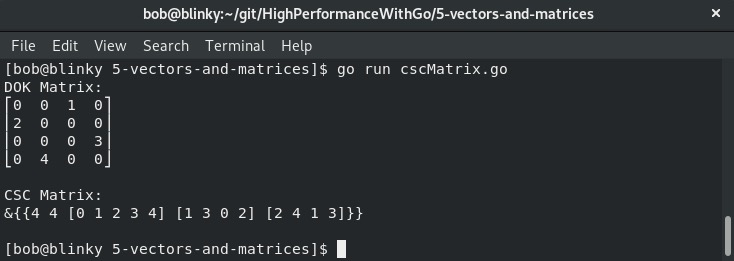
前面代码块的输出展示了DOK矩阵和CSC矩阵。在矩阵运算过程中，了解如何表示CSR和CSC矩阵至关重要。这两种不同类型的矩阵具有不同的特点。例如，DOK矩阵具有O(1)的访问模式，而CSC矩阵为提高效率采用面向列的运算方式。

总结

在本章中，我们讨论了矩阵和向量，以及这两种数据结构在实际中如何用于执行当今计算机科学领域中的大量数据运算。此外，我们还学习了基本线性代数子程序（BLAS）、向量、矩阵以及向量/矩阵运算。向量和矩阵是线性代数中常用的构建模块，我们通过实际示例了解了它们的应用场景。

本章讨论的示例在处理现实世界的数据运算时会有很大帮助。在第6章“编写易读的Go代码”中，我们将探讨如何编写易读的Go代码。能够编写易读的Go代码有助于清晰简洁地表达主题和思路，方便代码贡献者之间的协作。